학습 내용
- 선형회귀와 경사 하강법을 직접 손으로 구현해보며 과정을 이해한다
- 데이터 분석 및 모델링의 전체 과정을 이해한다
추가적으로 피처 엔지니어링도 진행하여 모델을 개선해보자
자세한 코드 보기 : https://github.com/seongyeon1/aiffel/blob/main/Exploration/Quest2/project1_sykim.ipynb
1. 데이터 가져오기
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
df_X = diabetes.data
df_y = diabetes.target2. 모델에 입력할 데이터 X 준비하기
import numpy as np
X = np.array(df_X)
X.shape
3. 모델에 입력할 데이터 X 준비하기
y = np.array(df_y)
4. train 데이터와 test 데이터로 분리하기
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
print(f"전체 학습 데이터: {X.shape} 레이블: {y.shape}")
print(f"학습 데이터: {X_train.shape} 레이블: {y_train.shape}")
print(f"테스트 데이터: {X_test.shape} 레이블: {y_test.shape}")
전체 학습 데이터: (442, 10) 레이블: (442,)
학습 데이터: (353, 10) 레이블: (353,)
테스트 데이터: (89, 10) 레이블: (89,)
5. 모델 준비하기
입력 데이터 개수는 column의 개수이므로 X.shape[1]이다.
따라서 가중치 W는 10개이고, b는 1개인데 b는 0으로, W는 모두 1의 벡터로 초기화해주었다.
W = np.ones(shape=(X.shape[1],))
b = 0모델 함수 구현하기
def model(X, y, epochs, learning_rate):
losses = []
weight_history = []
bias_history = []
W = np.ones(shape=(X.shape[1],))
b = 0
for epoch in range(epochs):
y_pred = X.dot(W) + b
l = loss(y, y_pred)
w_grad, b_grad = gradient(X, y, y_pred)
W -= learning_rate * w_grad
b -= learning_rate * b_grad
print(f'epoch {epoch + 1}, loss: {l}')
losses.append(l)
weight_history.append(W.copy())
bias_history.append(b)
return W, b, losses, weight_history, bias_history6. 손실함수 정의하기
mse를 사용하고자 한다
def loss(y, y_pred):
return ((y_pred - y) ** 2).mean()
7. 기울기를 구하는 gradient 함수 구현하기
def gradient(x, y, y_pred):
error = y_pred - y
w_grad = 2 * np.dot(x.T, error) / len(y)
b_grad = 2 * error.mean()
return w_grad, b_grad8. 하이퍼 파라미터인 학습률 설정하기
learning_rate = 0.8
9. 모델 학습하기
- 정의된 손실함수와 기울기 함수로 모델을 학습해주었다.
epochs = 10000W, b, losses, weight_history, bias_history = model(X_train, y_train, epochs, learning_rate)
10. 시각화 및 모델 개선
10-1. loss의 변화
plt.figure(figsize=(10, 3))
plt.subplot(1, 2, 1)
plt.plot(losses[:200])
plt.subplot(1, 2, 2)
plt.plot(losses[200:])
- 200 epoch 동안 30000에서 5000까지 떨어지고 200 epoch 이후에는 3150에서 2900대로 떨어진 것을 볼 수 있다
- epoch을 아무리 늘려도 2000정도 이후부터는 크게 줄어들지 않았다
10-2. 가중치(weight)의 변화
plt.figure(figsize=(10, 3))
plt.subplot(1, 2, 1)
plt.plot(weight_history)
plt.subplot(1, 2, 2)
plt.plot(weight_history[:200])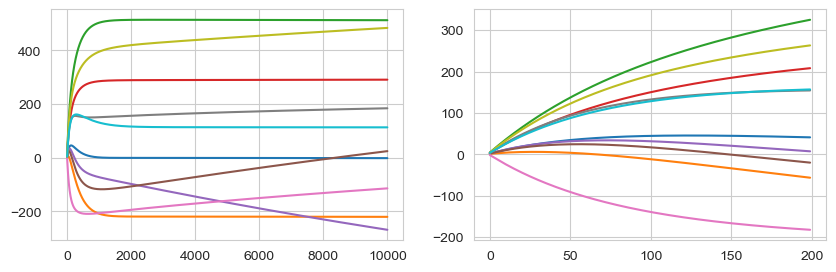
plt.plot(bias_history[:20])

loss, weight, bias 값들의 변화를 확인해본 결과
- 선형회귀 모델이 정보를 담아내는데에 한계가 있을 것이라는 판단이 되었다.
- 하지만 모델은 바꾸지 않는 하에서 최대치의 성능을 내는 것이 이번 프로젝트의 목적이였기에 데이터를 변형하고 feature engineering에 집중하고자 하였다.
모델 개선을 위한 데이터 분석 및 시각화
- 원래는 EDA를 더 앞에서 했어야 했지만 이번 프로젝트에 의해 어쩔 수 없이 baseline 수행 후에 진행하게 되었다.
피처 확인
train = pd.DataFrame(X_train)
train['label'] = y_train
train.describe()
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_minmax = scaler.transform(X_train)
# scaler.transform(X_test)
X_train_minmax = pd.DataFrame(X_train_minmax)
X_train_minmax.hist()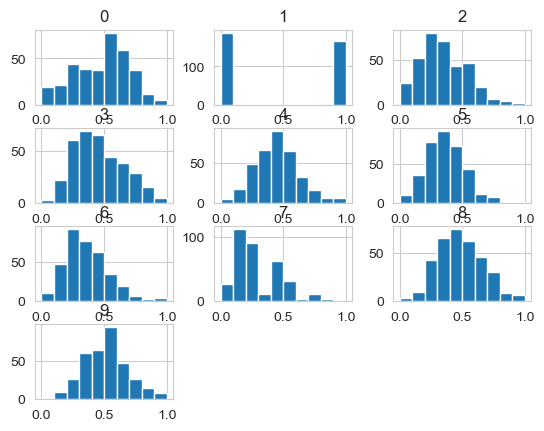
label 분포
plt.figure(figsize=(12, 4))
# 첫 번째 subplot
ax1 = plt.subplot(1, 2, 1)
sns.histplot(y_train, kde=True, ax=ax1)
ax1.set_title('Distribution of y_train')
# 두 번째 subplot
ax2 = plt.subplot(1, 2, 2)
sns.histplot(np.sqrt(y_train), kde=True, ax=ax2)
ax2.set_title('Distribution of sqrt(y_train)')
# 레이아웃 자동 조정
plt.tight_layout()
plt.show()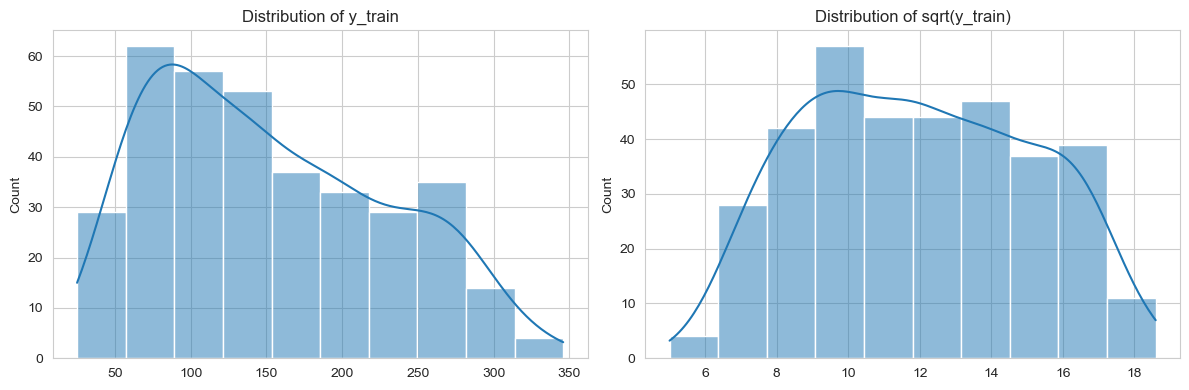
- 레이블의 경우는 살짝 왼쪽으로 치우쳐 보여서 root scaling을 진행해보았다.
- log scaling을 해보니 반대로 우로 치우치게 되어서 root scaling을 하였다.
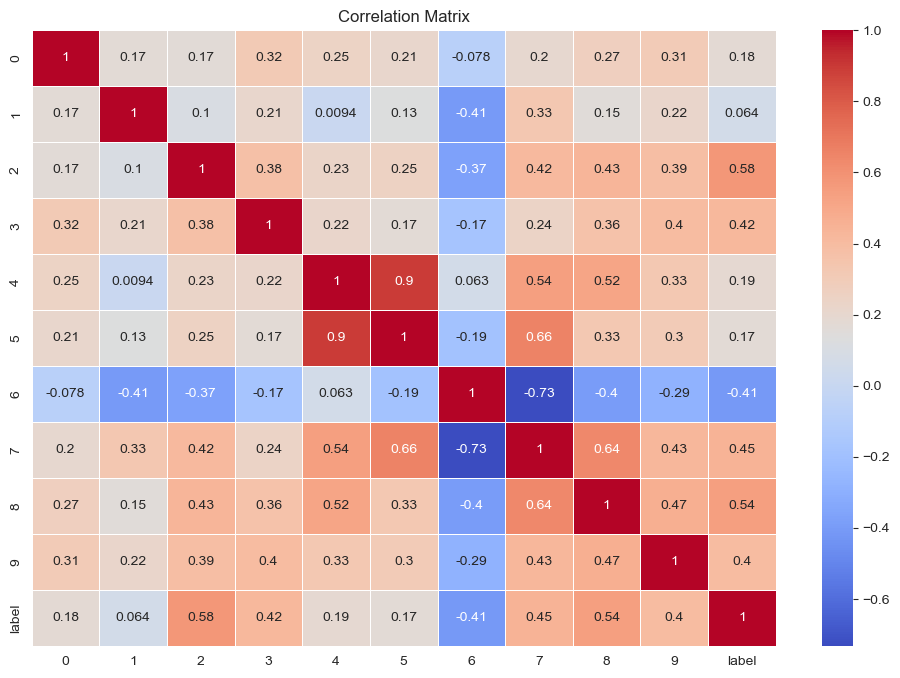
상관관계를 활용한 피처 선택
- 상관관계가 높지 않은 피처(상관계수가 -0.1 < r < 0.1처럼 타깃과의 상관관계가 매우 낮은 피처)는 예측에 도움이 되지 않을 수 있다.
- 이를 제거하거나 다른 피처와 조합하는 피처 엔지니어링을 고려할 수 있다
상관관계를 활용한 피처 선택
- 상관관계가 높지 않은 피처(상관계수가 -0.1 < r < 0.1처럼 타깃과의 상관관계가 매우 낮은 피처)는 예측에 도움이 되지 않을 수 있다.
- 이를 제거하거나 다른 피처와 조합하는 피처 엔지니어링을 고려할 수 있다
- 높은 상관관계 : 타깃과 높은 상관관계를 가진 피처가 중요한 피처일 가능성이 높음.
- 낮은 상관관계 : 타깃과의 상관관계가 낮은 피처는 모델에 큰 영향을 미치지 못할 수 있음.
- 피처 간 상관관계가 높은 경우 : 다중공선성(multicollinearity) 문제를 유발할 수 있으므로 주의. 다중공선성 문제가 있으면, 모델의 해석력이 떨어지고 예측 불안성이 커질 수 있음.
- 피처 제거 : 타깃과의 상관관계가 너무 낮거나 피처 간 상관관계가 너무 높은 피처들을 제거할 수 있다.
- 피처 결합 : 상관관계가 높은 피처들을 결합하여 새로운 파생 피처를 만들 수 있다.
- 차원 축소 : PCA(주성분 분석)를 사용하여 차원을 축소. 상관관계가 높은 피처들을 하나의 주성분으로 모아 모델의 효율성을 높임.
threshold = 0.1
low_corr_features = corr_with_target[abs(corr_with_target) < threshold].index
data_reduced = train_minmax.drop(columns=low_corr_features)
# 높은 상관관계 피처 확인
high_corr_pairs = corr_matrix[abs(corr_matrix) > 0.7].stack().reset_index()
high_corr_pairs = high_corr_pairs[high_corr_pairs['level_0'] != high_corr_pairs['level_1']]
print('Highly correlated pairs:\n', high_corr_pairs)
threshold를 정해 제거한 결과 피처 1을 없애주었다.
4.5번 피처
4, 5번 피처는 PCA를 진행한다.
from sklearn.decomposition import PCA
# PCA 적용
pca = PCA(n_components=1)
X_pca_45 = pca.fit_transform(data_reduced[[4,5]])
data_reduced.drop([4,5], axis=1, inplace=True)
data_reduced['pca_45'] = X_pca_456, 7, 8번 피처
6번 피처와 7번 피처가 상관관계가 있고 7번 피처와 8번 피처가 상관관계가 있으므로 7번 피처를 제거한다6번 피처와 7번 피처가 상관관계가 있고 7번 피처와 8번 피처가 상관관계가 있으므로 7번 피처를 제거한다
data_reduced = data_reduced.drop(7, axis=1)
최종 모델 학습
최종 모델 학습을 위해 테스트 데이터에도 같은 전처리를 진행해준다.
X_test = scaler.transform(X_test)
X_test = pd.DataFrame(X_test)
X_test.drop([1, 7], axis=1, inplace=True)X_pca_45 = pca.fit_transform(X_test[[4,5]])
X_test.drop([4,5], axis=1, inplace=True)
X_test['pca_45'] = X_pca_45y_train = np.sqrt(y_train)X_train_scaled = np.array(data_reduced.drop(['label'], axis=1))
y_train_scaled = np.array(y_train)W, b, losses, weight_history, bias_history = model(X_train_scaled, y_train_scaled, epochs=10000, learning_rate=0.1)
12. test 데이터에 대한 성능 확인하기
y_pred = np.dot(X_test, W) + b
# y 값 원래대로 변환
y_pred = y_pred ** 2
loss(y_test, y_pred)loss(y_test, y_pred)
13. 정답 데이터와 예측한 데이터 시각화하기
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.scatter(X_test[:, 0], y_test, color='blue', label='Actual')
plt.scatter(X_test[:, 0], y_pred, color='red', label='Predicted')
plt.xlabel('X_train\'s first column')
plt.ylabel('Target')
plt.title('Pred vs Truth')
plt.legend()
plt.show()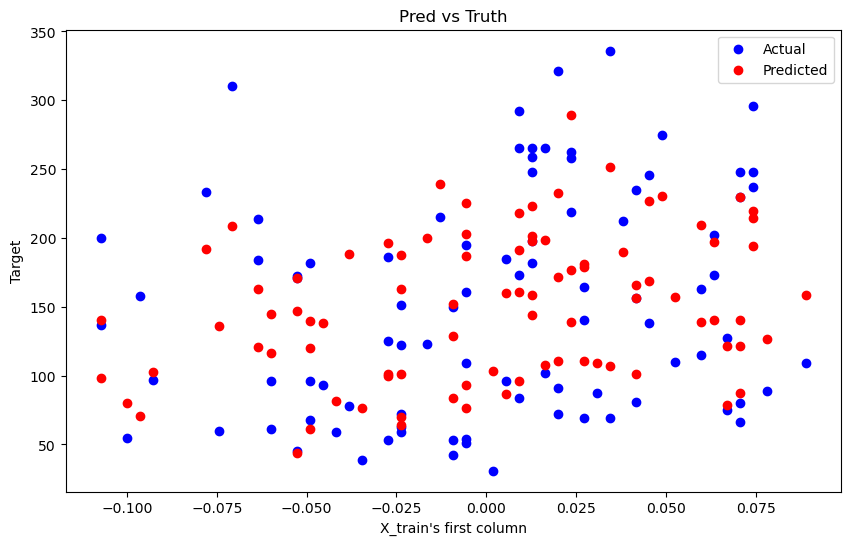
결론
- gradient descent 직접 구현하는 게 생각보다 함수를 나누는 것이 어려웠다. 클래스를 통해 구현해보고 싶다.
- 선형 회귀로는 한계가 있는 것 같다
- 생각보다 feature engineering을 열심히 한다고 성능이 많이 높아지지는 않는 것 같아서 아쉽다.
참고자료
손수 설계하는 선형회귀, 당뇨병 수치를 맞춰보자
'AIFFLE > PROJECT' 카테고리의 다른 글
| [CV] 인물사진 만들기 - 기본편 (OpenCV, semantic segmentation) (2) | 2024.06.08 |
|---|---|
| [CV] 고양이 수염 스티커 합성하기 (OpenCV 완전 정복기) (1) | 2024.06.08 |
| [kaggle] Bike Sharing Demand (자전거 수요 예측) (1) | 2024.05.28 |
| [kaggle] 포켓몬 분류하기 프로젝트 (Tree 모델들의 Feature importance를 확인해보자) (2) | 2024.05.28 |



