학습 내용
- Loss와 Metric
- Confusion Matrix 와 Precision/Recall
- Threshold의 변화에 따른 모델 성능
- Precision-Recall 커브
- ROC 커브
Loss와 Metric
loss와 metric은 단순히 수식의 차이로 설명할 수는 없다.
loss과 metric은 사용되는 시점과 용도가 다르다
- Loss : 모델 학습시 학습데이터(train data) 를 바탕으로 계산되어, 모델의 파라미터 업데이트에 활용되는 함수
- Metric : 모델 학습 종료 후 테스트데이터(test data) 를 바탕으로 계산되어, 학습된 모델의 성능을 평가하는데 활용되는 함수
RMSE(Root Mean Square Error) 라는 개념은 Loss 함수로도 사용되기도 하고, 회귀 모델의 Metric으로 사용되기도 한다.
그렇다면 Accuracy가 학습단계에 좋은 Loss가 될 수는 없을까?
결론적으로 Accuracy는 Loss가 될 수는 없다. Discrete한 Accuracy는 Continuous한 Cross Entropy에 비해, 파라미터가 학습되어야 할 방향을 정확하게 제시하지 못하기 때문이다.
이렇듯 대부분의 metric 함수는 loss 함수로 사용이 어렵다.
1. 대부분의 metric 함수는 불연속적이라 미분이 불가능한 형태이다. 하지만 모델 학습에 주로 사용되는 경사하강법 계열의 알고리즘들은 미분 가능한 함수를 필요로 하기에 metric을 그대로 사용하면 이 알고리즘들을 적용할 수 없게 된다.
2. metric 함수는 그 특성상 값의 변동이 크다.
- 이는 최적화 과정을 매끄럽지 못하게 만들어 학습을 방해하는 요인이 된다. 모델이 국소 최적점에 빠지거나 발산할 위험이 커진다.
3. 모델이 학습 데이터에만 과도하게 최적화되는 과적합 문제가 발생할 수 있다.
4. 마지막으로 일부 metric은 전체 데이터에 대해서만 계산 가능한 경우가 있어, 미니배치를 사용하는 학습 과정에 적용하기 어려울 수 있으며, 이는 계산 효율 측면에서도 좋지 않다.
그렇지만,
분류모델의 성능을 평가하는데는 Accuracy가 더 우월한 Metric이다.
궁극적으로 우리가 원하는 모델은 테스트 데이터에 대한 Accuracy가 높은 모델이지, Cross Entropy가 얼마나 낮아졌는지가 우리의 궁극적 관심은 아니기 때문이다.
하지만 모델의 정확성을 향상시켜 궁극적으로 Accuracy가 높은 모델을 만들기 위해 활용하는 Loss로는 Cross Entropy가 더욱 적당하다.
하지만, 회귀모델일 경우 RMSE가 Loss와 Metric 양쪽으로 효과적으로 사용될 수도 있다.
즉, Loss나 Metric으로 어떤 함수를 활용할지는 해결해야 할 Task에 따라 다르다
Confusion Matrix 와 Precision/Recall
- 분류 모델에서 Accuracy가 항상 좋은 Metric이 되지 않을 수 있다는 것을 알고 있다.
- 분류 모델 측면에서 모델의 결과가 이진 분류되는 형태일 때, 모델의 예측 결과와 실제 정답셋을 비교하여 아래의 표처럼 4가지 항목으로 표현하는 Confusion Matrix을 떠올려 보자

True Positive (TP) - 모델이 양성(Positive)을 양성으로 맞혔을 때
True Negative (TN) - 모델이 음성(Negative)을 음성으로 맞혔을 때
False Positive (FP) - 모델이 음성(Negative)을 양성(Positive)으로 잘못 예측했을 때
False Negative (FN) - 모델이 양성(Positive)을 음성(Negative)으로 잘못 예측했을 때
그러면 분류 모델 측면에서 우리가 아는 정확도(Accuracy) 는 전체 표본 중 정확히 분류된 표본의 수 라고 볼 수 있다.
즉, 이진 분류일 때 정확도를 아래의 식으로 표현할 수 있다.
정확도(Accuracy)=TP+TNTP+TN+FP+FN
멀티 클래스(multi-class)의 분류 결과를 하고 있다면, 표본의 결과를 정답, 오답으로 나누어 아래의 식으로 표현할 수 있다.
정확도(Accuracy)=(정답을맞힌예측의수)(전체문제의수)=TP+TNTP+TN+FP+FN
음성 대 양성 데이터 분포가 불균형할 경우 정확도는 모델을 평가하는데 좋은 척도가 되지 못한다
Precision과 Recall
- Precision은 정밀도, Recall은 재현율이라는 단어로 표시하지만, 단어 원래 의미를 충분히 표현하기 어려워 단어 자체를 그대로 사용하곤 한다.

정밀도(Precision)
정밀도(Precision)=TPTP+FP
- 모델이 양성으로 규정한 것이 얼마나 정확한지
- 모델이 음성으로 규정한 것에 대해서는 크게 관심이 없음
- 정밀도가 높다는 것은 FP가 낮다는 것
즉 모델이 양성으로 잘못 규정한 것이 적을수록 정밀도는 올라감.
재현율(Recall)
재현율(Recall)=TPTP+FN
- 실제로 양성인 것들이 얼마나 모델에 의해 정확하게 탐지되었나
- 실제로 음성인 것을 양성으로 잘못 규정한 것에 대해서는 관심이 없음
- 재현율이 높다는 것은 FN이 낮다는 것
즉 모델이 실제 양성을 분류해 내지 못한 경우가 적을 수록 재현율은 올라감.
Recall과 Precision을 최대화 하는 방법
- Precision은 FP를 0으로, Recall은 FN은 0으로 만들면 된다.
- 즉, 다른 값들의 변화를 신경쓰지 않는하에서 정밀도를 높인다 했을 때,
단순히 모든 값을 음성으로 예측해버려도 1이 되어 버리는 문제가 있다.
- 재현율도 마찬가지로 모두 양성으로 예측해버려도 1이 되어버린다.
쉽게 생각하기 위해 예를 들어보면 Precision은 주로 스팸메일, Recall은 암예측을 대표적인 예시로 드는데,
1) 스팸이 아닌걸 스팸으로 옮기지 않기위해 모든 메일을 스팸이 아니다라고 예측(Precision = 1)하는 사례
2) 암인 환자를 암이 아니라고 하는 경우를 막기위해 모든 환자에게 암이라 예측(Recall = 1)하는 사례로 생각하자.
- 위 사례처럼 예측을 하게 된다면 예측모델이 쓸모가 없어진다.
F-score
- 불균형 데이터가 주어진 상황에서 분류 모델을 평가하는데 유용한 척도
- F1 score : F score에서 β가 1이 될 때를 말합니다. F1 score는 Precision과 Recall의 조화평균이 되는 값으로서, Precision과 Recall 둘 다 고려할 수 있어서 분류 모델의 훌륭한 척도가 된다.
조화평균이 왜 좋은 척도인가? -이에 대해서는 추가적으로 포스팅을 할 계획이다.
Fβ=(1+β2)⋅precision⋅recall(β2⋅precision)+recall

Threshold의 변화에 따른 모델 성능
암환자 분류 모델을 생각해보면, 우리가 학습시킨 모델의 출력이 일정 이상 기준선(Threshold)를 넘어가면 우리는 양성이라고 분류하게 될 것이다. 그런데 우리가 학습시킨 모델은 Recall이 높을 수록 좋은 모델이다. 양성일 확률이 0.5가 넘으면 양성이라고 분류하게 하는 것보다는 양성일 확률이 0.3만 넘으면 양성이라고 분류하도록 해보면 어떻게 될까?
모델의 파라미터 등은 전혀 변한 것이 없는데, 모델의 출력값을 해석하는 방식만 다르게 해도 이 모델은 전혀 다른 성능을 가지게 된다.
따라서 이 모델의 성능척도 값도 달라지게 될 것이다.
즉, 모델의 성능이라는 것이 F1 score같은 숫자 하나로만 규정될 수 있는 게 아니라는 것을 의미하게 됩니다. (물론 모델 출력의 해석방식이 고정적으로 주어진다면 F1 score는 유효한 Metric이 된다.)
이렇게 Threshold가 달라지는 것을 고려하여 전체적인 모델의 성능을 평가하는 방법으로
1) PR(Precision and Recall) 커브와
2) ROC(Receiver Operating Characteristic) 커브를 그려보는 두가지 방법이 있다.
Threshold의 변화에 따라 모델 성능이 달라지는 상황을 간단한 분류 모델 예제를 통해 살펴 보자.
from sklearn import datasets
from sklearn.model_selection import train_test_split
import numpy as np
iris = datasets.load_iris()
X = iris.data
y = iris.target
print(X.shape) # 4개의 feature를 가진 150개의 데이터이다.
# 붓꽃 분류 예제는 상당히 간단하기 때문에, 그대로 훈련시키면 거의 100%에 가까운 성능을 내기에
# 일부러 데이터에 잡음(noise)을 추가해 성능을 낮추어서 진행하고자 한다.
# 랜덤한 값으로 이루어진 200 * n_features, 즉 800개의 컬럼을 매 데이터마다 추가한다다.
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
print(X.shape) # 804개의 feature를 가진 150개의 데이터가 되었다.
# 분석을 간단히 하기 위해 양성/음성으로 나뉘는 이진 분류(binary classification) 문제로 줄였다
#- 0, 1 라벨에 속하는 붓꽃 샘플만 사용하도록 제한합니다.
X_train, X_test, y_train, y_test = train_test_split(X[y < 2], y[y < 2],
test_size=.5,
random_state=random_state)
print("훈련, 테스트 셋에 사용된 라벨의 종류: {} ".format( set(y_test)))
print("훈련 데이터 shape :", X_train.shape)
print("테스트 데이터 shape :", X_test.shape)
훈련, 테스트 셋에 사용된 라벨의 종류: {0, 1}
훈련 데이터 shape : (50, 804)
테스트 데이터 shape : (50, 804)모델 학습
# SVM(Support Vector Machine)으로 모델을 구성
from sklearn import svm
classifier = svm.SVC(kernel='poly', random_state=random_state)
classifier.fit(X_train, y_train)
classifier.score(X_test,y_test)0.48
# `classifier.score()` 함수는 테스트데이터에 대한 평균 정확도(Accuracy)를 리턴한다
# SVM의 커널을 변경
classifier = svm.SVC(kernel='linear', random_state=random_state)
classifier.fit(X_train, y_train)
classifier.score(X_test,y_test)0.8
모델 뒤에 Softmax가 있어서 확률값을 출력하는 Logistic Regression 모델과는 달리, SVM에서 별도로 제공하는 decision_function() 함수가 존재한다. 이 함수값은 ( -1, 1) 범위값을 가지는데, 0보다 작으면 음성(label=0), 0보다 크면 양성(label=1)으로 분류하게 된다.
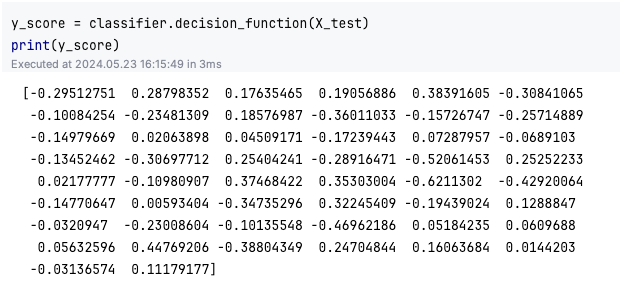
그럼 여기서 confusionmatrix를 계산해 보자.
실제 정답값 ytest와 ypred를 비교해 보면 다음과 같은 결과가 얻어진다.
confusionmatrix는 [[TN, FP], [FN, TP]]의 형태로 출력된다.
사이킷런에서는 icationreport이라는 함수를 통해 confusionmatrix에서 얻어진 TN, FP, FN, TP 값을 토대로 Precision, Recall, F1-score 등의 평가척도값을 계산해 준다.
from sklearn.metrics import confusion_matrix, classification_report
y_pred = classifier.predict(X_test)
conf_mat = confusion_matrix(y_test, y_pred)
print(conf_mat)
rpt_result = classification_report(y_test, y_pred)
print(rpt_result)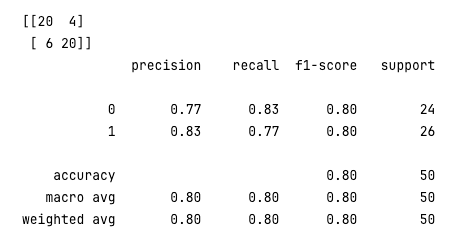
이제 threshold 를 바꿔보며 비교해보자
y_pred_new_threshold = classifier.decision_function(X_test) > -0.1
conf_mat = confusion_matrix(y_test, y_pred_new_threshold)
print(conf_mat)
rpt_result = classification_report(y_test, y_pred_new_threshold)
print(rpt_result)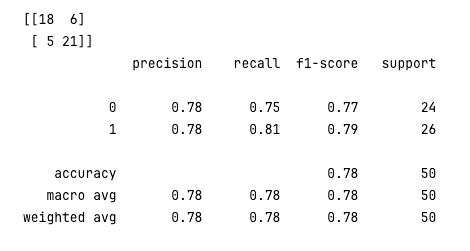
양성 분류 기준을 확대했기 때문에, Recall이 0.77에서 0.81로 상승했습니다. 하지만 전체적인 F1-score는 0.80에서 0.79로 소폭 하락했다. 하지만 일부 Task의 특성에 따라 위 결과가 더 좋은 결과를 낼 수도 있다.
Threshold 값을 조금씩 바꿔보면서 평가척도값이 어떻게 변하는지 확인해 보자
y_pred_new_threshold = classifier.decision_function(X_test) > -0.2
conf_mat = confusion_matrix(y_test, y_pred_new_threshold)
print(conf_mat)
rpt_result = classification_report(y_test, y_pred_new_threshold)
print(rpt_result)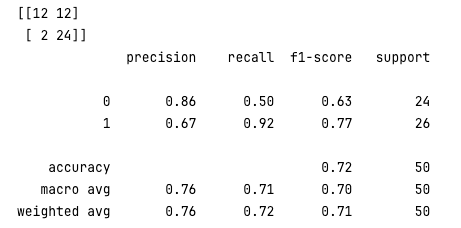
y_pred_new_threshold = classifier.decision_function(X_test) > 0.1
conf_mat = confusion_matrix(y_test, y_pred_new_threshold)
print(conf_mat)
rpt_result = classification_report(y_test, y_pred_new_threshold)
print(rpt_result)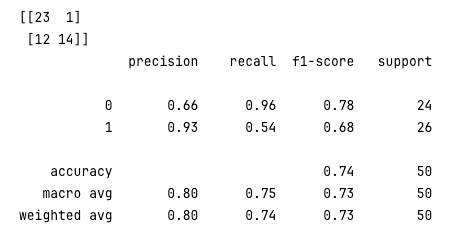
y_pred_new_threshold = classifier.decision_function(X_test) > 0.2
conf_mat = confusion_matrix(y_test, y_pred_new_threshold)
print(conf_mat)
rpt_result = classification_report(y_test, y_pred_new_threshold)
print(rpt_result)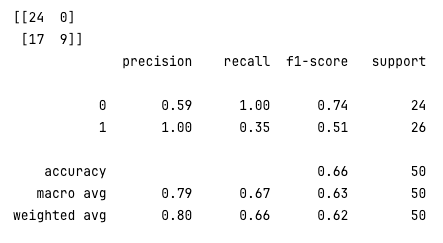
Precision-Recall 커브
이전 스텝에서 분류모델의 분류기준(Threshold)을 변경함에 따라 동일한 모델에서도 Precision, Recall 등 평가척도 값이 달라지는 것을 확인했다. PR(Precision-Recall) 커브는 Recall을 X축, Precision을 Y축에 놓고 Threshold 변화에 따른 두 값의 변화를 그래프로 그린 것이다.
from sklearn.metrics import PrecisionRecallDisplay
import matplotlib.pyplot as plt
disp = PrecisionRecallDisplay.from_estimator(classifier, X_test, y_test)
disp.ax_.set_title('binary class Precision-Recall curve: '
'AP={0:0.2f}'.format(disp.average_precision))
plt.show()
위 그림을 보면 Precision과 Recall 사이의 트레이드오프 관계를 확인할 수 있다.
Threshold값에 따라 우리가 얻게 되는 Precision, Recall 값은 저 그래프상의 어딘가가 될 것이다.
우리가 최종적으로 원하는 값은 Precision이든 Recall이든 모두 1에 가까운 값일 것이다.
그래서 Threshold 값에 무관하게 모델의 전체적인 성능을 평가하는 방법으로, 위 PR 커브 아래쪽 면적을 계산하는 방법이 있다.
이것을 AUC(Area Under Curve) 값이라고 합니다. PR AUC를 계산하는 방법으로 다음과 같이 사이킷런에서 제공하는 avera≥≺isionscore 함수를 사용한다.
sklearn.metrics.average_precision_score
(https://scikit-learn.org/stable/modules/generated/sklearn.metrics.average_precision_score.html)
AP=∑n(Rn−Rn−1)Pn
위 수식의 특성을 살펴보면, average_precision_score(AP) 값은, n 값을 무한히 크게 한다면 아주 작은 Recall 구간에 대해 Pn 값을 적분하는 것과 같게 된다.
그러므로 PR 커브의 아래쪽 면적인 PR AUC와 같은 의미가 된다.
하지만 사이킷런 문서에서는 avera≥≺isionscore와 PRAUC가 구현 측면에서 약간 다르다고 설명하고 있다.
두 개념이 의미적으로 비슷하게 사용될 수 있다고 이해하면 될 것 같다.
from sklearn.metrics import average_precision_score
average_precision = average_precision_score(y_test, y_score)
print('평균 precision-recall score: {0:0.2f}'.format(
average_precision))평균 precision-recall score: 0.91
ROC 커브
- ROC(Receiver Operating Characteristic Curve) 는 수신자 조작 특성 곡선이라는 단어로 표현할 수 있 다.
- ROC는 앞서 계산해보았던 Confusion Matrix 수치를 활용해, 분류기의 분류 능력을 그래프로 표현하는 방법이다.
- Threshold 값의 변화에 따른 Confusion Matrix가 변화하는 값들을 표현한다.
ROC 예시 곡선
ROC를 그리는 축인 TP Rate과 FP Rate은 Precision, Recall과 비슷해 보이지만 조금 다른 개념이다.
TP Rate과 FP Rate은 다음과 같이 계산합니다.
TPR(Sensitivity)=TPTP+FN
FPR(1−Specificity)=FPTN+FP
TP Rate(TPR)의 수식을 잘 보면 실은 우리가 잘 아는 Recall과 같은 것입니다.
FP Rate는 1-Specificity라고 소개되어 있는데, Specificity라는 것은 TNTN+FP
이 되므로, 실은 음성 샘플에 대한 Recall이라고 볼 수 있습니다.
https://youtu.be/4jRBRDbJemM?si=RV7bEqt-dYkhMxzt
- 사이킷런에는 roc_curve, auc 라는 함수를 통해 ROC를 그리거나 ROC AUC를 쉽게 구해볼 수 있다.
from sklearn.metrics import roc_curve, auc
fpr, tpr, _ = roc_curve(y_test, y_score)
roc_auc = auc(fpr, tpr)
plt.figure()
lw = 2
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
print(f"auc result:{roc_auc}")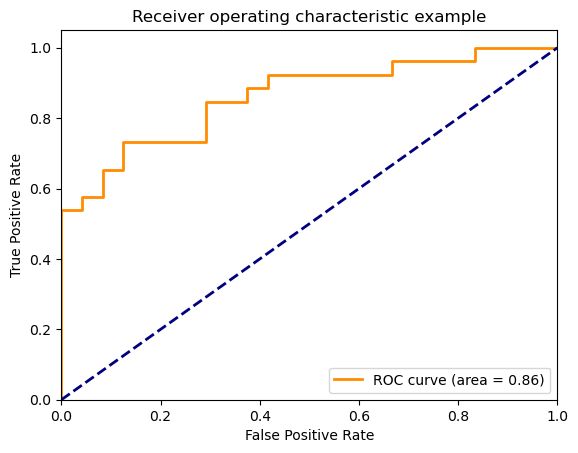
아주 이상적으로 Precision과 Recall이 전부 1이 되는 완벽한 모델이라면 ROC 커브에서는 바로 (0, 1)에 찍히게 된다.
양성과 음성에 대한 Recall이 모두 1이 될 테니 TPR은 1, FPR은 0이 될 것이다.
몇 가지 극단적인 경우를 생각해 보자.
모델이 모든 샘플에 대해 양성이라고 분류한다면 분류기가 (1, 1)에 찍힐 것이다.
반대로 모든 샘플에 대해 음성이라고 분류한다면 이 분류기는 (0, 0)에 찍힐 것이다.
완벽한 랜덤 분류기를 가정해 봅시다. 이 분류기는 양성이든 음성이든 무관하게 p의 확률로 양성이라고 분류할 것이다.
이 랜덤분류기의 Recall은 p가 될 것입니다. 음성에 대한 Recall도 p가 될 테니 이 분류기는 (p, 1-p)에 찍힐 것이다.
위 그래프에서 (0, 0)과 (1, 1)을 잇는 파란 점선은 바로 위와 같은 극단적인 경우들만 모아놓은 경우이다.
의미있는 분류기라면 적어도 이 파란 점선보다는 위쪽에 그려져야 하며, 가급적 (0, 1)에 가깝게 그려질 수록 우수한 분류기가 된다. 그러므로 ROC AUC가 클수록 상대적으로 좋은 성능의 모델이라고 할 수 있을 것이다.
ROC AUC 값도 최대 1이 될 수 있을 것이다.
# SVM 커널의 종류를 바꿔 가며 ROC 커브를 그리고 ROC AUC 값을 구하는 코드
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
# ROC 곡선을 그리기 위한 설정
plt.figure()
lw = 2
for k in kernels:
classifier = svm.SVC(kernel=k, random_state=random_state)
classifier.fit(X_train, y_train)
y_score = classifier.decision_function(X_test)
fpr, tpr, _ = roc_curve(y_test, y_score)
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, lw=lw, label=f'ROC curve for {k} (area = {roc_auc:.2f})')
# 기준선 추가
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
# 플롯 설정
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic for different kernels')
plt.legend(loc="lower right")
# 결과 표시
plt.show()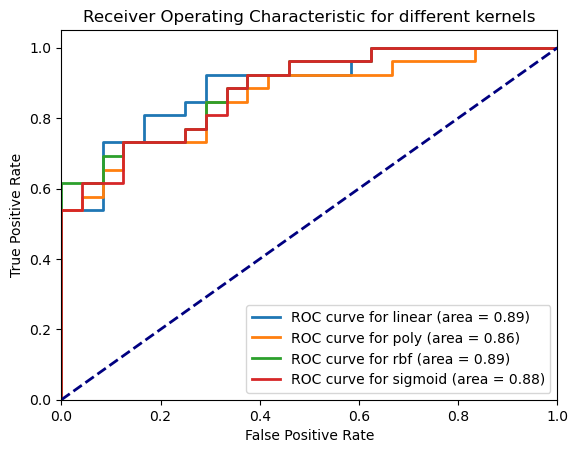
참고자료
https://modulabs.co.kr/blog/loss-versus-accuracy/
https://bioinformaticsandme.tistory.com/328
'AIFFLE > STUDY' 카테고리의 다른 글
| [DL] 사용자 정의 훈련 스탭 (fit 메서드 커스터마이즈 하기) (0) | 2024.06.02 |
|---|---|
| [DL] keras API (Sequential, Functional, Subclassing) 이해하기 (1) | 2024.06.02 |
| [DL] 일반화 성능 향상시키기 (0) | 2024.05.21 |
| 텐서의 이해 (0) | 2024.05.21 |
| 머신러닝과 딥러닝 (0) | 2024.05.21 |
